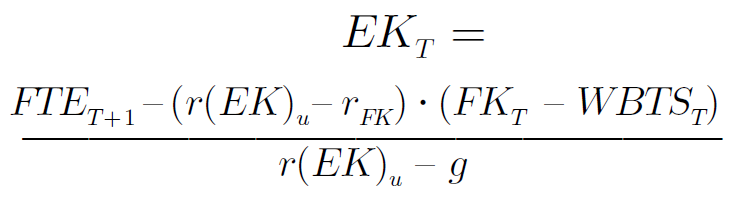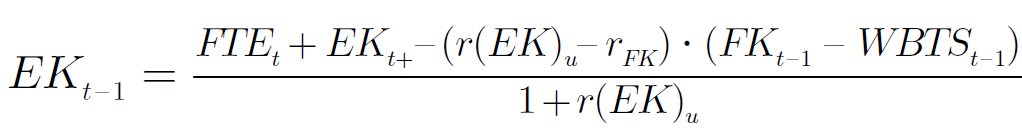Discounted Cashflow-Verfahren

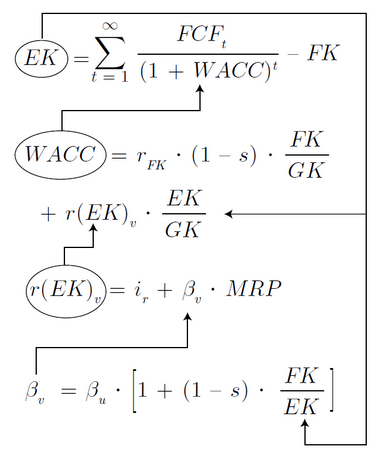
Zentrale Fragestellungen

Wie bereits bei der Darstellung der verschiedenen Bewertungsverfahren erläutert, wird bei allen DCF-Verfahren der Unternehmenswert durch Diskontierung (= Abzinsung) der periodenspezifischen Cashflows ermittelt. Damit lauten die zwei zentralen Fragen:

1.Welche Cashflows genau müssen verwendet werden?

2.Mit welchem Zinssatz sollen diese Cashflows abgezinst werden?

Beginnen wir mit der zweiten Fragestellung. Beim WACC-Ansatz werden zur Diskontierung der Free Cashflows die gewichteten Kapitalkosten (= WACC) herangezogen. Diese lassen sich als Summe aus den gewichteten Eigen- und Fremdkapitalkosten darstellen. In den gewichteten Kapitalkosten wird zusätzlich auch der Vorteil der steuerlichen Abzugsfähigkeit der Fremdkapitalzinsen (das sog. „Tax Shield“) berücksichtigt.

Für die gewichteten Kapitalkosten gilt:

WACC = Fremdkapitalkosten * Steuerkorrektur * Anteil FK + Eigenkapitalkosten * Anteil EK

bzw.

Erläuterungen zu den verwendeten Kürzeln finden Sie im Abkürzungsverzeichnis.

Für die Gewichtung ist bei EK bzw. FK auf die jeweiligen Marktwerte (nicht Buchwerte) abzustellen, wobei gilt: GK = EK + FK

Für die Ermittlung der Eigenkapitalkosten wird i.d.R. auf das Standardmodell der Kapitalmarkttheorie, das Capital Asset Pricing Model (= CAPM), zurückgegriffen. Dabei berechnen sich die Eigenkapitalkosten aus der Summe eines (quasi) risikolosen Basiszinssatzes zuzüglich einer unternehmensindividuellen Risikoprämie nach der Formel:

Eigenkapitalkosten = risikolose Rendite + Risikoprämie

= risikolose Rendite + β * Marktrisikoprämie

bzw.

Diese vergleichsweise einfache Formel zur Ermittlung der erwarteten Rendite einer Kapitalanlage (Summe aus risikolosem Zins und Risikoprämie) hat zwei wichtige Implikationen, deren Verständnis die Arbeit mit dem Beta-Faktor und dem CAPM erleichtern:

•Die Risikoprämie kann als Produkt aus Preis mal Menge verstanden werden. Der Preis des Risikos ist die durchschnittlich erwartete Marktrisikoprämie (MRP). Die Menge des Risikos wird durch den Beta-Faktor (β) erfasst.

•Es gibt mit dem Beta-Faktor nur einen einzigen wertrelevanten Parameter, der unternehmensspezifisch ist. Die übrigen Parameter sind sog. Marktparameter.

Der risikolose Basiszinssatz (ir) wird in der Regel aus dem Zinssatz öffentlicher, inländischer Anleihen mit einer festen Laufzeit von zehn oder mehr Jahren abgeleitet.

Hinsichtlich der Ermittlung der Risikoprämie wird im CAPM zwischen dem unsystematischen Risiko und dem systematischen Risiko unterschieden. Das unsystematische Risiko kann ein einzelner Investor grundsätzlich durch Diversifikation seines Portfolios aus unterschiedlichsten Anlagen (z.B. Aktien) reduzieren. Folglich wird eine Risikoprämie nur für das systematische, allgemeine Marktrisiko bezahlt (= Marktrisikoprämie bzw. MRP). Für eine Schätzung der künftig erwarteten Marktrisikoprämie wird auf die historische Differenz zwischen einem Aktienindex (z.B. DAX) und der Rendite (quasi) risikoloser Kapitalmarktanlagen zurückgegriffen (MRP = rM - ir). Dabei stellt rM die Rendite eines risikobehafteten, aber breit diversifizierten Marktportfolios und ir die risikofreie Rendite dar.

Das systematische Risiko wird über den sog. Beta-Faktor gemessen. Der Beta-Faktor gibt dabei den Risikobeitrag einer Investitionsmöglichkeit (z.B. Aktie) im Vergleich zu dem allgemeinen Marktrisiko wieder. Ein Beta-Faktor größer Eins bedeutet, dass das (systematische) Risiko der zu bewertenden Investition größer als das Marktrisiko ist und die Rendite der Investition stärker als die Marktrendite schwankt; ein Beta-Faktor kleiner Eins bedeutet dementsprechend, dass die Rendite der Investition weniger als die Marktrendite schwankt und das Risiko somit kleiner als das Marktrisiko ist.

Der Beta-Faktor lässt sich aus Daten des Kapitalmarktes ableiten. Mathematisch ausgedrückt ist das Beta die Kovarianz einer Aktie zum Gesamtmarkt, geteilt durch die Varianz der Renditen des Gesamtmarktes. Falls das Bewertungsobjekt nicht börsennotiert ist, muss dieser indirekt hergeleitet werden. Im letztgenannten Fall erfolgt die Bestimmung über eine so genannte Peer Group. Die Peer Group umfasst eine Auswahl von börsennotierten Unternehmen, mit denen das Bewertungsobjekt hinsichtlich seiner Chancen- und Risikostruktur vergleichbar ist. Dabei ist sowohl das operative Risiko als auch das Finanzierungsrisiko relevant. Die Höhe des Beta-Faktors ist somit auch abhängig von der Kapitalstruktur des zu bewertenden Unternehmens. In der Regel werden sich die Kapitalstrukturen des Bewertungsobjekts und der Vergleichsunternehmen voneinander unterscheiden, so dass eine Anpassung des Beta-Faktors der Peer Group an die Kapitalstruktur des Bewertungsobjekts (= Levering) vorzunehmen ist. Dabei wird der Beta-Faktor der Vergleichsunternehmen um das Kapitalstrukturrisiko bereinigt (= Unlevering). Der unverschuldete Beta-Faktor der Peer Group wird anschließend dem Verschuldungsgrad des Bewertungsobjekts (zu Marktwerten) angepasst (= Relevering).

Die zur Ermittlung der gewichteten Kapitalkosten erforderlichen Fremdkapitalkosten (rFK) errechnen sich als gewogener durchschnittlicher Kostensatz der einzelnen zinstragenden langfristigen Verbindlichkeiten des zu bewertenden Unternehmens. Dem CAPM zufolge entsprechen sich (wegen der unterstellten rigiden Modellannahmen) Fremdkapitalkosten und der risikolose Basiszinssatz (rFK = ir). Die Fremdkapitalgeber tragen beim CAPM insofern keine operativen Risiken. Diese Annahme ist in der Realität regelmäßig nicht gegeben, weil die Fremdkapitalkosten in der Praxis den risikolosen Basiszinssatz übersteigen (rFK > ir). Fremdkapitalgeber fordern somit ebenfalls eine Risikoprämie zum risikolosen Basiszinssatz (siehe Hinweis-Box "Praxis-Info" weiter unten).

Steuerliche Abzugsfähigkeit der Fremdkapitalzinsen

Eine Besonderheit des Bruttoansatzes stellt die Berücksichtigung des Vorteils der steuerlichen Abzugsfähigkeit der Fremdkapitalzinsen als Betriebsausgabe dar. Im Rahmen des WACC-Ansatzes wird der Free Cashflow bei vollständiger Eigenfinanzierung berechnet, so dass der Ertragsteuervorteil (sog. Tax Shield) aus der Abzugsfähigkeit von Finanzierungsaufwendungen von den ertragsteuerlichen Bemessungsgrundlagen auf Unternehmensebene (Gewerbesteuer u. Körperschaftsteuer bei Kapitalgesellschaften) nicht im Free Cashflow enthalten ist. Zum Ausgleich werden dagegen die Fremdkapitalkosten um den Ertragsteuervorteil reduziert. Es ergibt somit:

Fremdkapitalkosten = rFK * (1-s)

mit s = Unternehmenssteuersatz (in %)

Zusammenfassung und Zirkularitätsproblem:

Im Ergebnis errechnen sich die gewogene Kapitalkostensätze im WACC-Ansatz durch die Gewichtung der Eigenkapitalkosten mit der Eigenkapitalquote und der Fremdkapitalkosten (steuerkorrigiert) mit der Fremdkapitalquote. Um den gewichteten Kapitalkostensatz zu berechnen, muss jedoch die in Marktwerten gemessene Kapitalstruktur (d.h. EK u. FK) bekannt sein. Da der Marktwert des Eigenkapitals - der Unternehmenswert - im Zuge der Bewertung erst ermittelt werden muss, besteht somit beim WACC-Ansatz grundsätzlich ein (lösbares) Zirkularitätsproblem (siehe folgende Abbildung).

Zum Vergrößern Bild anklicken

Abbildung: Zirkularitätsproblem im WACC-Ansatz

Quelle: Alexander Enzinger/Peter Kofler: Das Roll-Back-Verfahren zu Unternehmensbewertung - Zirkularitätsfreie Unternehmensbewertung bei autonomer Finanzierungspolitik anhand der Equity-Methode In: Bewertungspraktiker Nr. 4, 2011, S. 2–10.

Erläuterungen zu den verwendeten Kürzeln finden Sie im Abkürzungsverzeichnis.

Beim WACC-Ansatz ergeben sich zwei Zirkularitäten. Zum einen ist der Verschuldungsgrad auf Marktwertbasis (FK/EK) für die Ermittlung der Renditeforderung der Eigenkapitalgeber für das verschuldete Unternehmen erforderlich. Zum anderen sind die Gewichtungsfaktoren bei der Ermittlung des gewogenen durchschnittlichen Kapitalkostensatzes (WACC) vom zu suchenden Bewertungsergebnis abhängig (siehe Abbildung oben). Ist kein Verschuldungsgrad auf Marktwertbasis vorgegeben (= wertorientierte Finanzierungspolitik), sondern handelt es sich wie in Unternehmensplanungen üblich um eine autonome Finanzierungspolitik (d.h. die zukünftigen Fremdkapitalbestände werden in absoluter Höhe geplant), dann führt das WACC -Verfahren progressiv nicht zirkularitätsfrei zu einem Bewertungsergebnis.

Folgende grundsätzliche Lösungsmöglichkeiten für diese Zirkularitätsproblematik bieten sich an:

1.Verwendung konstanter gewogener Kapitalkosten

2.Annahme einer konstanten Zielkapitalstruktur

3.Iterationsfunktion in Excel

4.Roll-Back-Verfahren

Verwendet man konstante gewogene Kapitalkosten (Pkt 1.) bzw. unterstellt eine konstante Zielkapitalstruktur (Pkt. 2) ist die Zirkularitätsproblematik nicht existent. Allerdings sind diese Annahmen realitätsfern und damit praxisuntauglich.

Die Aktivierung der Iterationsfunktion in Excel (Pkt 3.) ist zwar eine Lösungsmöglichkeit, verbietet sich aber aufgrund der Grundsätze der ordnungsgemäßen Erstellung von Finanzmodellen (vgl. FAST-Financial-Modelling-Standard), da dadurch ggf. andere Modellfehler unentdeckt bleiben könnten.

Wir haben uns deshalb im EFT Value Pack für die vierte Möglichkeit, nämlich die Berechnung mittels Roll Back-Verfahren entschieden.

Im Rahmen des Roll-Back-Verfahrens wird der Unternehmenswert ausgehend vom Wert der ewigen Rente Periode für Periode rückwärts bis zum Bewertungsstichtag ermittelt (= rekursive Unternehmenswertermittlung). Das oben erläuterte Zirkularitätsproblem wird bei diesem Verfahren durch formale Äquivalenzumformungen der Bewertungsgleichungen aufgelöst.

Aufgrund unterschiedlicher Prämissen bei der Anpassung von Beta-Faktoren können unterschiedliche Beta-Anpassungsformeln abgeleitet werden. Korrespondierend dazu, können entsprechende Roll-Back-Formeln abgeleitet werden (vgl. Alexander Enzinger/Peter Kofler: Das Roll-Back-Verfahren zu Unternehmensbewertung, Bewertungspraktiker Nr. 4, 2011, S. 2–10). Dabei ist zwischen der Detailplanungsphase sowie der ewigen Rente zu differenzieren.

In einem ersten Schritt wird der Marktwert des Eigenkapitals der ewigen Rente bestimmt. Für diese Berechnung wird im EFT Value Pack die Formel von Modigliani/Miller und Hamada verwendet, die davon ausgeht, dass das Risiko der Tax Shields dem Risiko des Fremdkapitals entspricht. Die entsprechende Roll-Back-Formel für die ewige Rente lautet:

Im nächsten Schritt wird der Marktwert des Eigenkapitals in der letzten Periode vor der ewigen Rente ermittelt, indem die korrespondierende Roll-Back-Formel für den Detailplanungszeitraum verwendet wird:

Erläuterungen zu den verwendeten Kürzeln finden Sie im Abkürzungsverzeichnis. Wird die gezeigte Rechentechnik rekursiv bis zur ersten Periode angewendet, ergibt sich der Marktwert des Eigenkapitals zum Bewertungszeitpunkt.

Relevante Cashflows

Aufgrund der bereits erläuterten konzeptionellen Unterschiede der Bruttoverfahren (= Entity-Ansätze) und der Nettoverfahren (= Equity-Ansatz), sind zur Unternehmenswertbestimmung jeweils andere Cashflows zugrunde zu legen.

Bei den Entity-Ansätzen ist auf den sog. Free Cashflow (= FCF) abzustellen. Dabei handelt es sich um die liquiden Mittel, die allen Kapitalgebern, also Eigenkapital- und Fremdkapitalgebern, zur Verfügung stehen. Im Gegensatz dazu sind beim Equity-Ansatz nur die Zahlungsströme relevant, die ausschließlich den Eigenkapitalgebern zur Verfügung stehen (= FTE bzw. Flow to Equity).

Der Free Cashflow wird in der Regel ausgehend vom Jahresüberschuss/Jahresfehlbetrag indirekt nach folgendem Schema ermittelt:

Im EFT Value Pack gehen wir vom Flow to Equity (FTE) aus, da dieser einfach einer der bereits vorhandenen Übersichten entnommen werden kann. Anschließend wird dieser nach dem folgenden Prinzip zum FCF übergeleitet.

In umgekehrter Weise ließe sich natürlich auch aus dem FCF der jeweilige FTE ableiten.

Im Rahmen der Annahmen zur DCF-Bewertung lässt sich die Unternehmensbewertung grundsätzlich aktivieren bzw. deaktivieren (Hinweis: Dies gilt dann auch für die Multiplikator-Verfahren). Im Fall einer Deaktivierung müssen keine weiteren Eingabefelder gelöscht werden. Auf den relevanten Übersichtsblättern erfolgt ein Hinweis, dass die Unternehmensbewertung ausgeschaltet wurde.

Die Berechnungen zur Unternehmensbewertung basieren im EFT Value Pack (immer) auf Jahren. Sofern aber aufgrund ihrer Vorgaben das erste Jahr kürzer als 12 Monate ist (z.B. bei einem Rumpfgeschäftsjahr), bekommen Sie einen entsprechenden Hinweis angezeigt. In diesem Fall sind die Berechnungen nicht exakt, da auch für das erste (kürzere) Jahr komplett abgezinst wird.

Unterhalb der Aktivierungs- bzw. Deaktivierungsfunktionalität wird ihnen nach dem Einschalten angezeigt, auf wie vielen Detailplanungsjahren ihre Berechnungen basieren (entspricht automatisch der von ihnen auf dem Blatt „Annahmen“ gewählten Modelllänge).

Auf Basis der Ergebnisse des letzten Detailplanungsjahres erfolgt - ggf. unter Berücksichtigung einer inflationsbedingten Wachstumsrate - die Ableitung der nachhaltigen finanziellen Überschüsse für die Phase der ewigen Rente. Das Jahr ab dem das Modell mit diesem „eingeschwungenen Zustand“ rechnet, wird ebenfalls ausgewiesen (vgl. Screenshot oben).

Der folgende Screenshot zeigt einen Überblick über die bewertungsrelevanten Annahmen für alle im EFT Value Pack enthaltenen DCF-Verfahren:

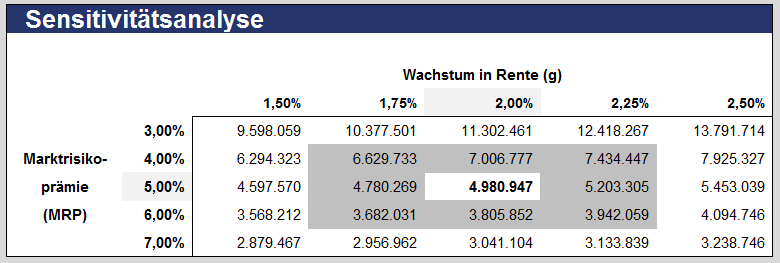
Die auf der rechten Seite befindlichen Annahmen für die Sensitivitätsanalyse steuern die Ausgestaltung und Generierung der folgenden Übersicht:

Sofern sich der vom Modell ermittelte Unternehmenswert (der auf den auf der linken Seite gemachten "Annahmen für Bewertung" basiert) in der (formattechnisch hervorgehobenen) Mitte der Sensitivitätsanalyse befinden soll, müssen Sie bei „Ausgangswert Wachstum (g)“ sowie bei „Ausgangswert MRP“ auf der rechten Seite die gleichen Werte wie auf der linken Seite vorgeben (siehe auch Kommentar in den genannten Eingabezellen sowie Beispiel in den Screenshots oben).

Einige kurze Hinweise zu den einzelnen bewertungsrelevanten Annahmen:

Wachstumsrate der ewigen Rente

Während das Wachstum in der Detailplanungsphase direkt in der Unternehmensplanung und somit in den finanziellen Überschüssen abgebildet wird, erfordert die Ermittlung eines nachhaltigen Wachstums in der zweiten Phase (= ewige Rente) zunächst eine eingehende Analyse auf der Basis langfristig zu prognostizierender (branchenspezifischer) Wachstumstrends und die Berücksichtigung der damit verbundenen Investitionserfordernisse.

Das unterstellte Wachstum der finanziellen Überschüsse muss sich nicht auf Preissteigerungen (Inflation) begrenzen. Auch ein längeres Wachstum z.B. durch steigende Produktabsätze ist möglich. Der Wachstumsabschlag kann dann über der Inflationsrate liegen.

Wachsen die finanziellen Überschüsse unendlich lange mit konstanter Rate, wird im Modell bei der Barwertermittlung der erste finanzielle Überschuss dieser Reihe mit einem um die Wachstumsrate verminderten Kapitalisierungszinssatz diskontiert (= Wachstumsabschlag). Die nachhaltige Wachstumsrate kann bei den Annahmen in Prozent eingegeben werden.

Risikoloser Zinssatz

Für den objektivierten Unternehmenswert ist bei der Bestimmung des Basiszinssatzes (= risikoloser Zinssatz) von dem landesüblichen Zinssatz für eine (quasi-)risikofreie Kapitalmarktanlage auszugehen. Daher wird für diesen Basiszinssatz grundsätzlich auf die langfristig erzielbare Rendite öffentlicher Anleihen ohne Ausfallrisiko abgestellt (vgl. IDW S.1 Tz. 116 ff.).

Der Fachausschuss für Unternehmensbewertung und Betriebswirtschaft (FAUB) des IDW hat aufgrund der anhaltenden Niedrigzinsphase eine Empfehlung für die Vorgehensweise bei der Rundung des Basiszinssatzes ausgesprochen. Bei Zinssätzen kleiner 1,0% ist auf 0,10% zu runden. Bei Zinssätzen größer 1,0% kommt die ursprüngliche Empfehlung des FAUB zum Tragen nach der auf 0,25% gerundet wird.

Der Basiszinssatz wird i.d.R. monatlich aktualisiert (und i.d.R. sogar kostenfrei im Internet publiziert). Zum 1. März 2020 betrug der vom IDW empfohlene (gerundete) Wert 0,20%.

Fremdkapitalkosten

Die Fremdkapitalkosten spiegeln die von den Gläubigern (i.d.R. Banken oder öffentliche Kreditinstitutionen) erwarteten Renditen wider. Da zukünftige Renditen wie bei den Eigenkapitalkosten schlecht beobachtbar sind, werden Fremdkapitalkosten üblicherweise anhand von historischen oder heute beobachtbaren Renditen approximiert. Dabei kommen grundsätzlich zwei Varianten infrage:

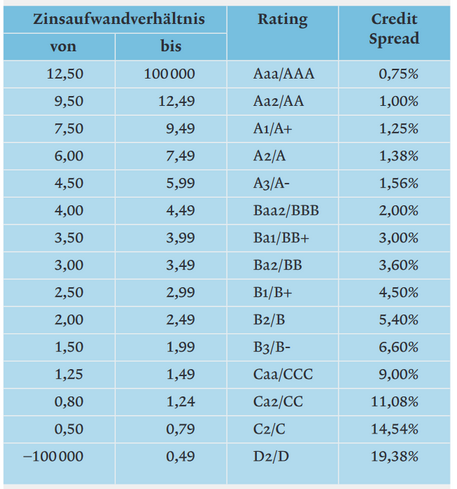
Bei der zweiten Variante lassen sich die Fremdkapitalkosten mittels eines auf Basis von börsengehandelten Obligationen abgeleiteten Credit Spreads herleiten:

rFK = ir + Credit Spread

Dabei wird in Abhängigkeit des Ratings ein durchschnittlich beobachtbarer Credit Spread herangezogen. Falls für das Bewertungsobjekt kein Rating vorliegt, was bei KMU üblicherweise der Fall sein dürfte, lässt sich mittels Zinsaufwandverhältnis ein sogenannt synthetisches Rating bestimmen:

Anhand dieser Verhältniszahl kann dann die entsprechende Rating-Klasse und der korrespondierende Credit Spread aus aufbereiteten Marktdaten abgelesen werden (siehe folgende beispielhafte Abb. für Industrieunternehmen). Die jeweiligen Credit Spreads sind branchenabhängig und ändern sich im Zeit- bzw. Konjunkturverlauf.

Zum Vergrößern Bild anklicken

Abbildung: Beispiel - Zinsaufwandverhältnisse, Ratings und Credit Spreads für Industrieunternehmen (Quelle: Damodaran 2019)

Marktrisikoprämie

Zur Schätzung der Marktrisikoprämie dienen langfristige Untersuchungen z.B. für den deutschen Kapitalmarkt. Vor dem Hintergrund der aktuellen Kapitalmarktsituation, die sich u.a. durch ein im historischen Vergleich weiterhin sehr niedriges Zinsniveau sowie eine expansive Geldpolitik der EZB auszeichnet, hat der FAUB des IDW im 4. Quartal 2019, seine Empfehlung zum Ansatz der Marktrisikoprämie (vor persönlichen Steuern) auf 6,00% bis 8,00% (Mittelwert 7,00%) angehoben.

Beta unverschuldet

Während der risikolose Zinssatz und die Marktrisikoprämie grundsätzlich für alle Unternehmen in einem bestimmten Land gleich sind, ist der Betafaktor unternehmensspezifisch. Er bringt zum Ausdruck, ob eine Unternehmung einem höheren systematischen Risiko ausgesetzt ist als der Gesamtmarkt (Beta > 1,0), dem gleichen (Beta = 1,0) oder einem kleineren (Beta < 1,0), das Unternehmen also stärker, gleich stark oder weniger stark schwankt als der Gesamtmarkt.

In der Praxis wird der Betafaktor typischerweise aus Kapitalmarktdaten abgeleitet. Das Beta entspricht dem Steigungsparameter einer linearen Regression von Aktienrenditen auf Marktrenditen. Da für KMU keine Aktienrenditen vorliegen, lässt sich das Beta nicht direkt berechnen, sondern muss alternativ geschätzt werden. Dies geschieht in der Praxis üblicherweise durch Bezug auf vergleichbare börsennotierte Unternehmen (= Peer Group). Die Auswahl der Vergleichsunternehmen sollte sich dabei primär an der Branchenzugehörigkeit orientieren sowie unter Berücksichtigung weiterer Kriterien wie geografischer Fokus, Größe, Kostenstruktur, Produkte, Lebenszyklus ect.

Im EFT Value Pack ist die Eingabe des unverschuldeten (unlevered) Beta für das Bewertungsobjekt erforderlich. Da es sich bei den mittels Kapitalmarktdaten gemessenen Betas aber um levered Betas handelt und die Kapitalstruktur des Bewertungsobjekts i.d.R. von der der Vergleichsfirmen abweicht, sind die Daten vor Verwendung als Inputwert im Tool mittels „Unlevering“ in unverschuldete Betas zu überführen.

Im Rahmen der Berechnungen im vorliegenden Bewertungsmodell erfolgt dann automatisch ein „Relevering“ des Beta auf Basis des jeweiligen Verschuldungsgrades bzw. der Kapitalstruktur des Bewertungsobjekts. Dabei geht das Modell für Zwecke des „Relevering“ grundsätzlich von einer autonomen Finanzierungspolitik aus. Ferner wird angenommen, dass das Risiko der Tax Shields dem Risiko des Fremdkapitals entspricht (vgl. Modigliani/Miller und Hamada).

Die folgende Formel wird zur Ermittlung des levered Equity Beta (= ßv = Beta verschuldet) verwendet:

Zugrundeliegende Prämissen:

βTS = βFK        Das Risiko der Tax Shields entspricht dem Risiko des Fremdkapitals

rFK ≥ ir                Die Fremdkapitalkosten müssen nicht dem risikolosen Zinssatz entsprechen

βFK ≥ 0                Auch anwendbar, wenn das Fremdkapital nicht risikolos ist

g ≥ 0                Wachstum in der ewigen Rente kann berücksichtigt werden

Unternehmenssteuersatz

Im Bewertungsmodell des EFT Value Pack werden auch Unternehmenssteuern (= Ertragsteuern, also Körperschaftsteuer und Gewerbesteuer bei Kapitalgesellschaften) berücksichtigt. Dies ist u.a. wegen der steuerlichen Abzugsfähigkeit der Fremdkapitalzinsen (sog. Tax Shields) im Rahmen der Ermittlung der gewichteten Kapitalkosten wichtig.

Der Unternehmenssteuersatz wird automatisch auf Basis der steuerlichen Eingaben auf dem Blatt „Annahmen“ ermittelt und ist kein Eingabefeld. Soll ggf. mit einem anderen Satz bei der Bewertung gerechnet werden, kann die Formel in dieser Zelle mit einem beliebigen Wert/Prozentsatz überschrieben werden (vorher ggf. Blattschutz entfernen).

Eine Berücksichtigung von persönlichen Steuern (z.B. der Einkommensteuer) im Rahmen der Bewertung erfolgt in diesem Modell nicht.